Hi pot haver matemàtiques en una obra d’art?

Introduïu l’escenari d’aquest itinerari explicant que aquesta setmana la classe de la colla de tercer està estudiant diferents obres d’art. Avui l’Andreu els ensenya el quadre del pintor madrileny Juan Gris titulat El carràs de raïm, que va pintar l’any 1924.

Comenceu observant la pintura i proposeu-los aquestes preguntes: Què s’hi representa, en aquest quadre? Reconeixeu la fruita que hi ha dibuixada? On està col·locada la fruita? Quina forma té aquest bol? I la cullera? Quines formes hi predominen, línies rectes o corbes? Hi reconeixeu cap altra figura geomètrica?

Demaneu als nens i les nenes que les responguin per parelles en el seu quadern i, després, corregiu-les en veu alta. Segurament, els nens i les nenes hauran dit que en el quadre hi predominen les línies rectes i les formes geomètriques. Aprofiteu per explicar que aquest quadre és cubista i que el cubisme és un moviment artístic que es caracteritza per convertir la realitat en formes simples, com petits cubs i altres formes geomètriques. Un altre pintor cubista molt conegut va ser Pablo Picasso... El coneixeu?

Expliqueu als nens i les nenes que al llarg de la setmana estudiareu diferents quadres de pintors cubistes i aprendreu a reconèixer totes les matemàtiques que hi ha representades.

Recordeu als nens i les nenes que les línies que segueixen sempre una mateixa direcció s’anomenen rectes i que les altres s’anomenen corbes. A més a més, tota línia pot ser oberta o tancada.

Per introduir les línies rectes i corbes, cada alumne ha de buscar a l’aula aquests dos tipus de línies. Fins i tot poden buscar-les en el seu cos. En acabar, cada alumne n’indicarà una de cada tipus.

Feu grups de 2, 3, 4, 5 i 6 alumnes, doneu-los un tros llarg de corda o cordill i proposeu-los que intentin fer línies tancades. S’adonaran que els grups de dos alumnes no podran i que els altres utilitzaran tants segments com elements té el grup.

Els alumnes poden fer servir el programa de dibuix Paint de l’ordinador i dibuixar línies corbes i rectes, tant obertes com tancades.

També podeu projectar amb la PDI la galeria d’imatges, perquè els nens i les nenes diferenciïn les línies rectes, corbes, tancades, obertes...

A continuació, llegiu en veu alta el quadre informatiu que explica les característiques de l’art cubista i proposeu als alumnes que resolguin l’activitat 1, en què han de dibuixar una de les corbes obertes i una de les corbes tancades de la pintura que ensenya l’Andreu. En acabar, alguns mostraran quines línies han escollit i dibuixat.

Pot ser interessant reflexionar col·lectivament sobre el cubisme per conèixer l’opinió dels nens i les nenes sobre aquest estil pictòric. Així, proposeu-los que responguin, en grups de quatre, les preguntes de l’activitat 2.

Entreu a “Les estovalles” per conèixer aquest altre quadre de Juan Gris.

Deixeu-los el temps pertinent i, després, feu una posada en comú per comentar les respostes de totes les preguntes.

Si el temps ho permet, proposeu als nens i les nenes que facin una rotllana al pati i que, de dos en dos, vagin sortint al mig. Col·loqueu un alumne a cada punta i digueu-los que, amb una regadora, facin una recta i una corba que vagi de l’un a l’altre (un s’espera i l’altre es mou fent una recta o una corba).

ATENCIÓ A LA DIVERSITAT

Per acompanyar i repassar

Línies obertes i tancades  Activitat per observar el dibuix d'entrada i trobar les línies obertes i tancades.

Línies  Activitat interactiva sobre les línies obertes i tancades.

Línies rectes i línies corbes  Activitat interactiva sobre línies rectes i corbes.

Demaneu a un voluntari que llegeixi en veu alta el quadre informatiu amb les definicions de recta, semirecta i segment. També podeu projectar amb la PDI la informació, en què hi ha els continguts explicats d’una manera ordenada i clara.

Tot seguit, en l’activitat 3, els alumnes repassaran els conceptes apresos. Després, feu una posada en comú a la pissarra per resoldre els possibles errors conceptuals de l’alumnat.

En l’activitat 4, es practica la diferència entre recta, semirecta i segment. Podeu resoldre aquesta activitat col·lectivament mitjançant la tècnica de treball cooperatiu “Estructura 1-2-4”. En grups de 4 alumnes, llegeixen l’enunciat de la primera pregunta i cada alumne, individualment (1), pensa la resposta i l’escriu. Tot seguit, de dos en dos (2), comparteixen les respostes i intenten arribar a una conclusió comuna. Finalment, tot el grup (4) posa en comú les respostes i formula la resposta final conjuntament. Es repeteix el procediment per a les altres cinc preguntes. En acabar l’activitat, demaneu als alumnes quines dificultats han tingut.

ATENCIÓ A LA DIVERSITAT

Per anar més enllà

Recta, semirecta i segment  Activitat per treballar els conceptes de recta, semirecta i segment a partir de dues fotografies.

Semirecta  Activitat per treballar el concepte de semirecta a partir d'una fotografia.

Recta, punt, semirecta i segment  Activitat interactiva sobre els conceptes de recta, punt, semirecta i segment.

Comenceu aquest bloc introduint la suma de segments amb una activitat lúdica, ja que és una manera de fer atractives les matemàtiques. Cada alumne pot imaginar que el seu braç és la suma de dos segments: el que va de l’espatlla al colze i el que va del colze al canell. Després, han de representar el braç com a suma de dos segments i apuntar-ne el valor.

A continuació, llegiu el quadre informatiu de l’activitat 5, en què s’explica com se sumen i es resten dos segments. Els alumnes trobaran més informació en el manual de consulta.

Tot seguit, demaneu als nens i les nenes que, per parelles, resolguin l’activitat 5. Podeu guiar l’activitat amb preguntes com aquestes: Quant mesura l’alçada de cada edifici? Quin és el més baix? I el més alt? Com els ordenaríeu?

Ara pot ser un bon moment per manipular els ItiCubs i trobar-hi segments (les arestes, i els que delimiten les pestanyes), corbes tancades (la que delimita el forat), i fer-ne més, per exemple traçant els segments diagonals de les cares.

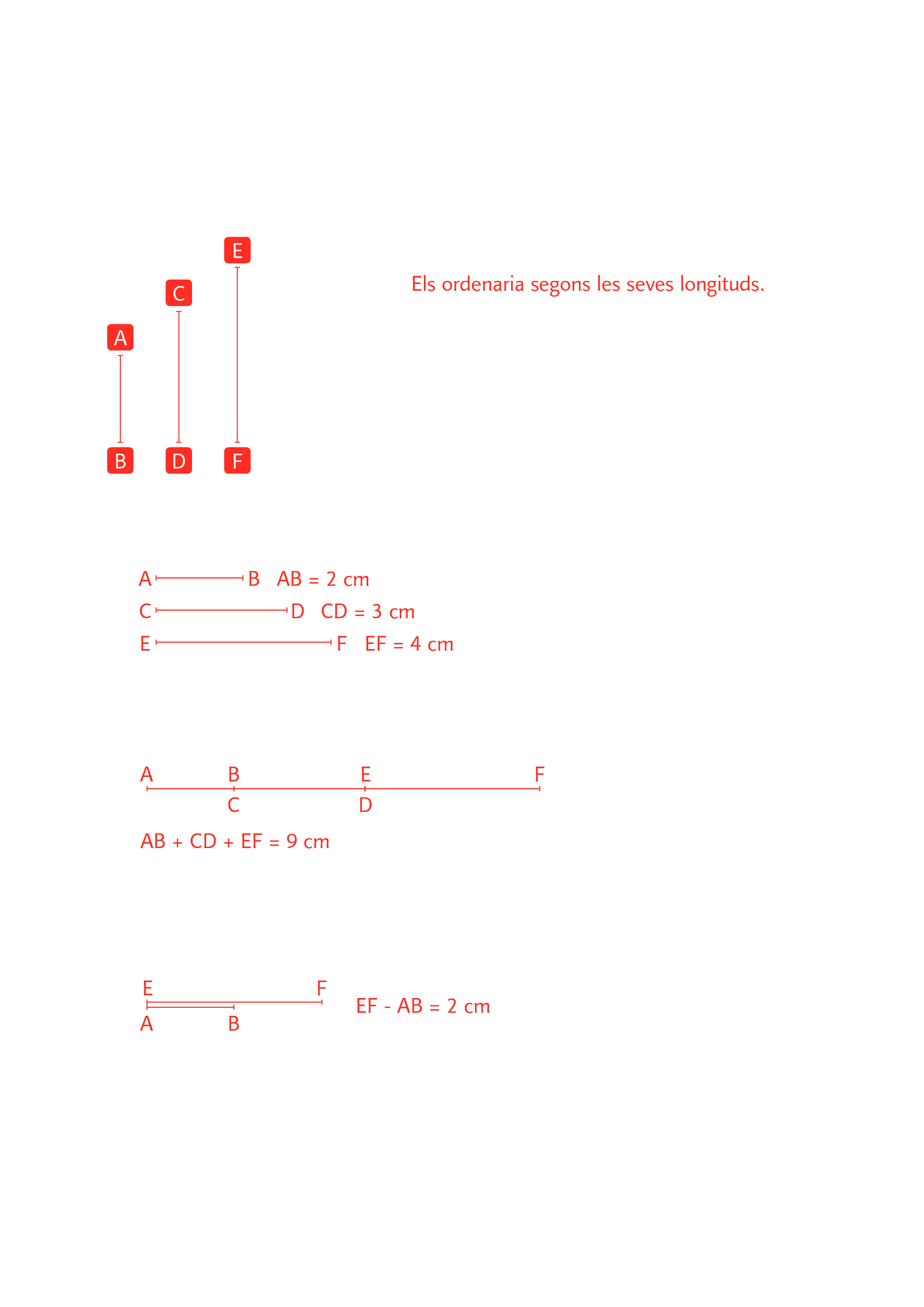
Podeu fer una suma de tres segments a la pissarra per resoldre els possibles errors conceptuals de l’alumnat. Si els quatre edificis mesuren 2, 3, 4 i 5 cm, respectivament, i trieu els 3 primers, la suma serà un segment de 9 cm.

Els alumnes hauran de comprovar que, per sumar, han de col·locar els segments l’un al costat de l’altre i, en canvi, per restar, l’un sobre l’altre. Quant dona la resta entre el segment més llarg i el més curt? Hauran de col·locar el segment de 2 cm sobre el de 5 cm, fent-ne coincidir els extrems esquerres, i veure que el resultat és 3 cm.

Si ho trobeu oportú, també poden dibuixar i mesurar els tres segments en què es pot considerar dividit cadascun dels dits de la seva mà. Després, han de representar gràficament els tres segments i la seva suma i han de fer les sumes numèriques corresponents.

Igualment, digueu-los que considerin la cama (des de l’engonal fins al turmell) com a segment AB i la cuixa (des de l’engonal fins al genoll) com a segment CD i demaneu-los que representin i calculin el segment resta DB (des del genoll fins al turmell).

ATENCIÓ A LA DIVERSITAT

Per anar més enllà

Segment  Activitat per treballar el concepte de segment a partir de l'Iticub.

Comenceu aquest bloc de continguts plantejant aquestes preguntes als nens i les nenes: Quina era la pregunta inicial d’aquest itinerari? L’heu respost resolent les activitats que heu fet fins ara?

Segurament diran que sí, ja que en els quadres cubistes han vist formes rectes i corbes i han reconegut diferents figures geomètriques.

Comenteu-los que en aquest bloc d’activitats treballaran els sentits per aprendre a reconèixer formes geomètriques en diferents obres artístiques.

Demaneu als nens i les nenes que observin el quadre La guitarra de l’activitat 6 i que responguin les preguntes individualment. Després, alguns voluntaris llegiran les seves respostes en veu alta i les corregirem oralment.

Podeu resoldre l’activitat 7 col·lectivament, aplicant la tècnica de treball cooperatiu “Llapis al centre”. Feu grups de 3 alumnes i assigneu-los una de les preguntes de l’activitat. Els alumnes, individualment, busquen la informació i escriuen la resposta. Deixeu-los el temps necessari. Després, un alumne llegirà la resposta en veu alta i els seus companys hauran de consensuar si és correcta o no. Durant aquest temps, els llapis seran al centre de la taula. Una vegada escollida la resposta, cada un agafarà el seu llapis i l’escriurà en el seu quadern. Se seguirà el mateix procediment per a les altres dues preguntes. Finalment, feu una posada en comú per resoldre els possibles dubtes de l’alumnat i responeu oralment la reflexió de la Sara: Per què creieu que diu que tindria més la sensació de muntar a cavall?

ATENCIÓ A LA DIVERSITAT

Per acompanyar i repassar

Línies de tots els tipus  Activitat per treballar els conceptes de línies corbes i tancades, recta, semirecta i segment a partir d’un quadre cubista de Juan Gris.

En l’activitat 8, els nens i les nenes hauran de dibuixar una pintura cubista. El fet que sigui una activitat lúdica facilita l’aplicació del que han après sense gairebé adonar-se’n, divertint-se, cosa que contribueix al seu aprenentatge. Us recomanem, doncs, que no en prescindiu.

Després, cada alumne pot explicar als seus companys quin és el títol de la seva pintura i què ha volgut representar. Si ho creieu oportú, podeu votar les cinc pintures més originals.

Aprofiteu l’activitat 9 per reflexionar en forma de pluja d’idees sobre la pregunta repte d’aquest itinerari: Hi pot haver matemàtiques en una obra d’art? Aneu anotant a la pissarra les idees i les reflexions que us semblin més interessants.

Per sistematitzar i consolidar els continguts treballats, proposeu als alumnes que facin l’itijoc.

Per acabar, valoraran el treball, l’aprenentatge de la setmana i la manera com s’han organitzat per resoldre les activitats individuals: Quines dificultats heu tingut? Heu necessitat ajuda del docent o d’algun company? Com heu treballat? En què podeu millorar? Us ha semblat interessant aprendre geometria amb pintures cubistes? Us seran útils aquests coneixements? Per què?

Aquesta petita secció de metaaprenentatge és important perquè ajuda a fer-los conscients no només del que aprenen, sinó de com ho estan aprenent.

ATENCIÓ A LA DIVERSITAT

Per acompanyar i repassar

Fitxa REPASSA Activitats per consolidar diferents continguts treballats en l’itinerari.

Per anar més enllà

Fitxa AMPLIA Activitats per ampliar diferents continguts treballats en l’itinerari.